Researchers Bruce Stephenson and Robin Macomber have uncovered a fascinating pattern of convergent discovery in the mathematics of critical phenomena across diverse fields. Their study, “Convergent Discovery of Critical Phenomena Mathematics Across Disciplines: A Cross-Domain Analysis,” reveals that techniques for detecting critical phenomena—phase transitions where correlation length diverges and small perturbations have large effects—have been independently developed across at least eight fields over nine decades.
The study highlights how different disciplines have developed equivalent techniques without cross-domain awareness. For instance, physicists use the correlation length \(ξ\), cardiologists rely on the DFA scaling exponent \(α\), financial analysts employ the Hurst exponent \(H\), and machine learning engineers utilize the spectral radius \(χ\). Despite the different notations and terminologies, all these measures essentially detect the same critical signatures. This convergence is a testament to the fundamental nature of critical phenomena mathematics.
Stephenson and Macomber’s research spans biomedicine, finance, machine learning, power systems, and traffic flow, among other fields. Their analysis of citation patterns from 1987 to 2010 shows minimal cross-domain awareness during this formative period. Researchers in these fields developed similar techniques independently, each tailored to their specific needs and terminologies. This independent discovery across disciplines strengthens the argument that criticality mathematics is a fundamental public knowledge, with significant implications for cross-disciplinary education and research accessibility.
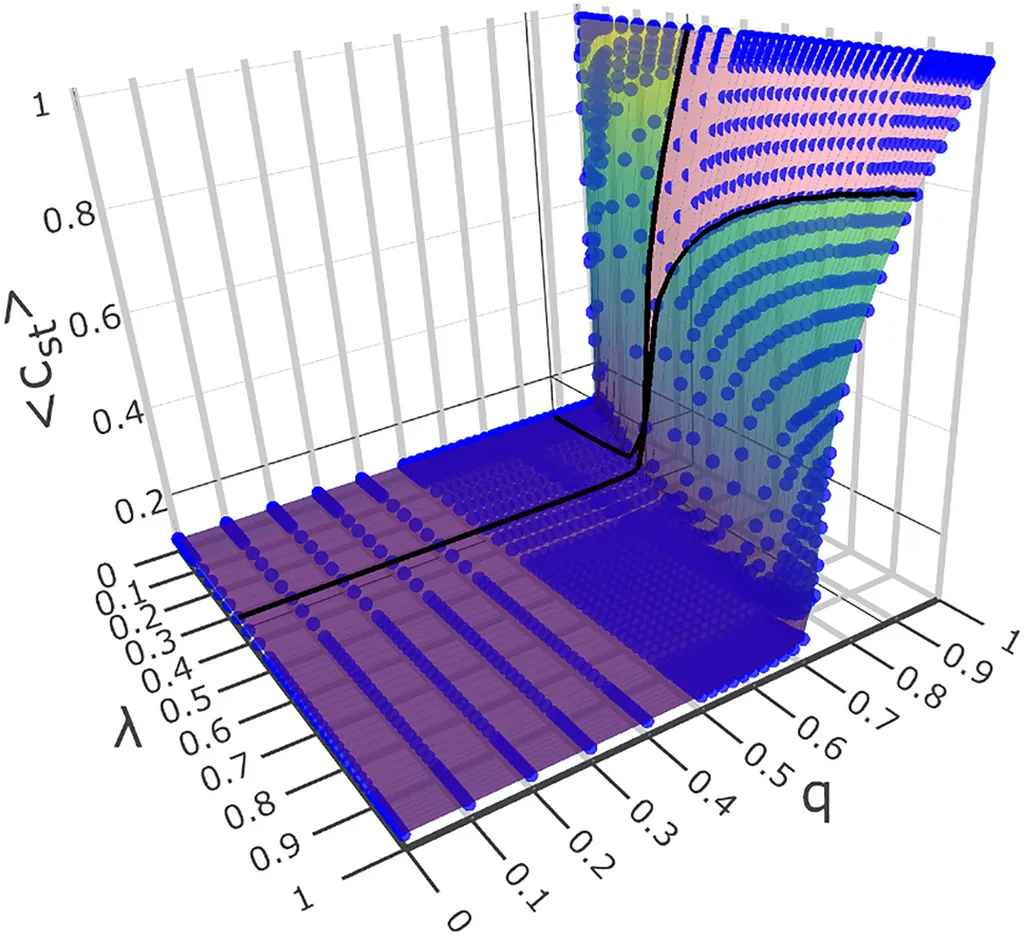
The researchers introduce Metatron Dynamics, a framework derived from distributed systems engineering, as a candidate ninth independent discovery. This framework not only strengthens the convergence pattern but also underscores the pervasive nature of critical phenomena across various domains. To validate their findings, the researchers tested correspondence on the 2D Ising model, confirming that measures from multiple frameworks correctly identify the critical regime at \(T_c = 2.269\).
The implications of this research are profound. By establishing criticality mathematics as a universal concept, Stephenson and Macomber argue for a more integrated approach to education and research. Their work suggests that understanding critical phenomena could bridge gaps between disparate fields, fostering collaboration and innovation. The inclusion of a plain-language summary in Appendix B ensures that non-specialist readers can grasp the significance of these findings, making the research accessible to a broader audience.
This study not only highlights the beauty of convergent discovery but also paves the way for a more unified understanding of critical phenomena across disciplines. As researchers continue to explore and validate these findings, the potential for cross-disciplinary collaboration and innovation grows, promising advancements in various fields from biomedicine to finance and beyond. Read the original research paper here.